Корреляционный анализ — определение степени и направления связи между двумя явлениями. Суть анализа заключается в расчете коэффициента корреляции.
Коэффициент корреляции (чаще всего под ним подразумевают коэффициент Пирсона) — это число в диапазоне от −1 до 1.
Коэффициент не связан с конкретными единицами измерения, а значит, подходит для сравнения любых величин. Например, можно определить взаимосвязь между расходами на интернет-маркетинг в рублях и посещаемостью сайта. Или между числом продающих рассылок и продажами в штуках.
При этом коэффициент корреляции просто вычислить, и он наглядно показывает связь между двумя переменными и ее направление.
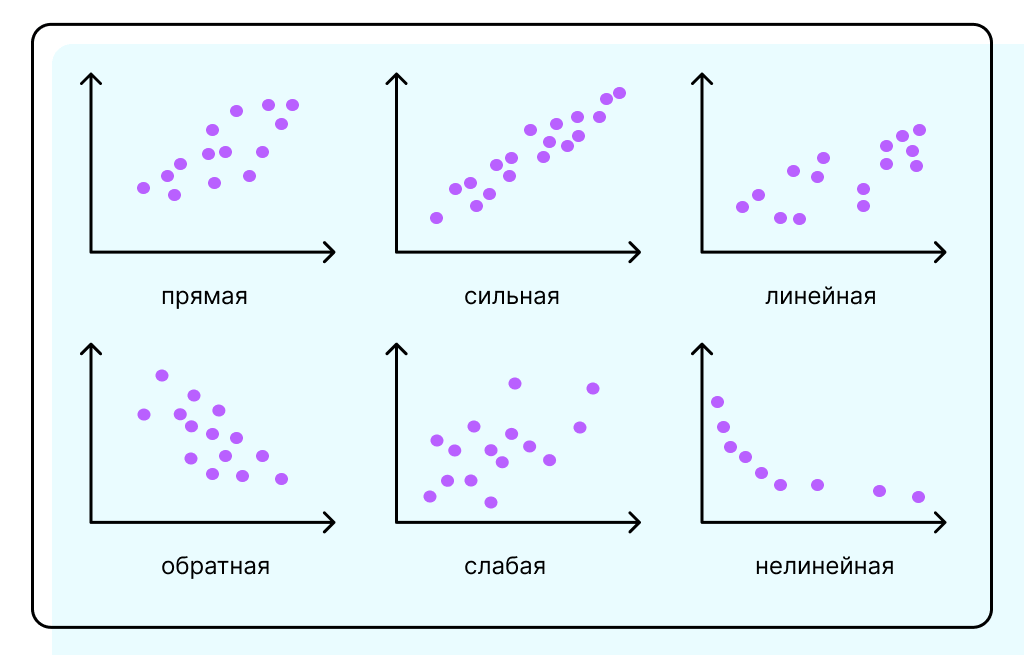
Наглядно корреляцию отображают с помощью диаграмм рассеяния. В Excel их можно построить, выбрав «Вставка-Диаграммы-Точечная»
Чем ближе коэффициент к 1, тем сильнее положительная связь между двумя переменными. Коэффициент корреляции = 1 означает, что изменению одной переменной соответствует такое же изменение другой.
Если коэффициент получается отрицательным, это означает обратную взаимосвязь: то есть при увеличении одной переменной, другая уменьшается.
Близкая к нулю корреляция показывает, что статически значимая взаимосвязь между двумя переменными отсутствует.
Зачем корреляцию используют в маркетинге
Корреляционный анализ помогает маркетологам решить большое количество самых разных задач. Если есть переменные, которые, как предполагает маркетолог, связаны друг с другом, то эту связь всегда можно проверить с помощью корреляции.
Приведем несколько примеров, когда корреляция будет полезна:
Оценить эффективность работы. Кажется, что чем больше предприниматель тратит на маркетинг, тем лучше должны быть бизнес-показатели. Но если корреляция между затратами и прибылью слабая или отрицательная, то это повод задуматься о величине и направлении вложений.
Помимо общей эффективности с помощью корреляции можно оценить, окупаются ли вложения в отдельные направления, например в SEO (корреляция затрат и конверсии на сайте) или рекламу у блогеров (затрат и продаж).
Спрогнозировать поведение потребителей. Например, чтобы рекомендовать зрителю подходящие фильмы, онлайн-кинотеатр должен понимать его вкусы. Такую информацию можно получить благодаря оценкам. Тогда можно определить корреляцию между оценками конкретного зрителя и других пользователей и показывать ему подборку картин, которые высоко оценили зрители со схожими вкусами. При этом чем больше пользователь ставит оценок, тем точнее алгоритмы предугадывают его предпочтения, а значит, тем проще удержать клиента в сервисе.
Разработать ценовую политику. Для обычных товаров работает правило: если цены падают, то продажи растут. Но есть товары Гиффена и Веблена для которых эта закономерность не действует. Корреляция с помощью прошлых данных по сбыту поможет определить, к каким группам относятся конкретные товары. Это пригодится при планировании скидок и других маркетинговых мероприятий, связанных с ценообразованием.
Как вычислить корреляцию
В Excel корреляцию можно вычислить с помощью функций КОРРЕЛ или PEARSON.
Обратите внимание, что аномальные показатели в данных (выбросы или пропуски) могут исказить значение коэффициента корреляции. Поэтому не забудьте провести их предварительную очистку.
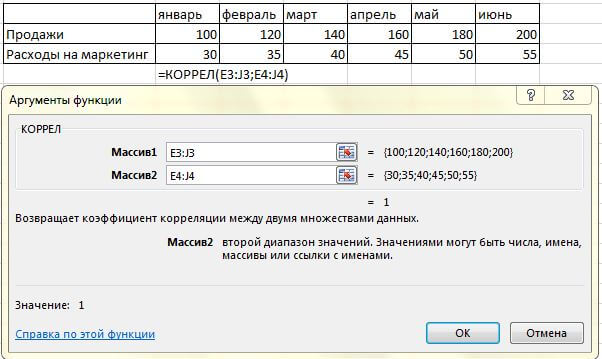
Пример вычисления корреляции между объемом продаж и расходами на маркетинг
Анализ корреляции часто дополняют исследованием регрессии — проводят корреляционно-регрессионный анализ.
Регрессия позволяет предсказать значение одной переменной (зависимой) под влиянием изменения другой (независимой) или нескольких других переменных. При этом исследователь сам определяет, какую переменную считать зависимой, а какую нет.
Например, если маркетолог обнаружил сильную положительную корреляцию между затратами на рекламу (независимая переменная) и продажами (зависимая переменная), то он может построить уравнение регрессии для прогнозирования того, насколько вырастет сбыт, если расходы на рекламу увеличатся на единицу.
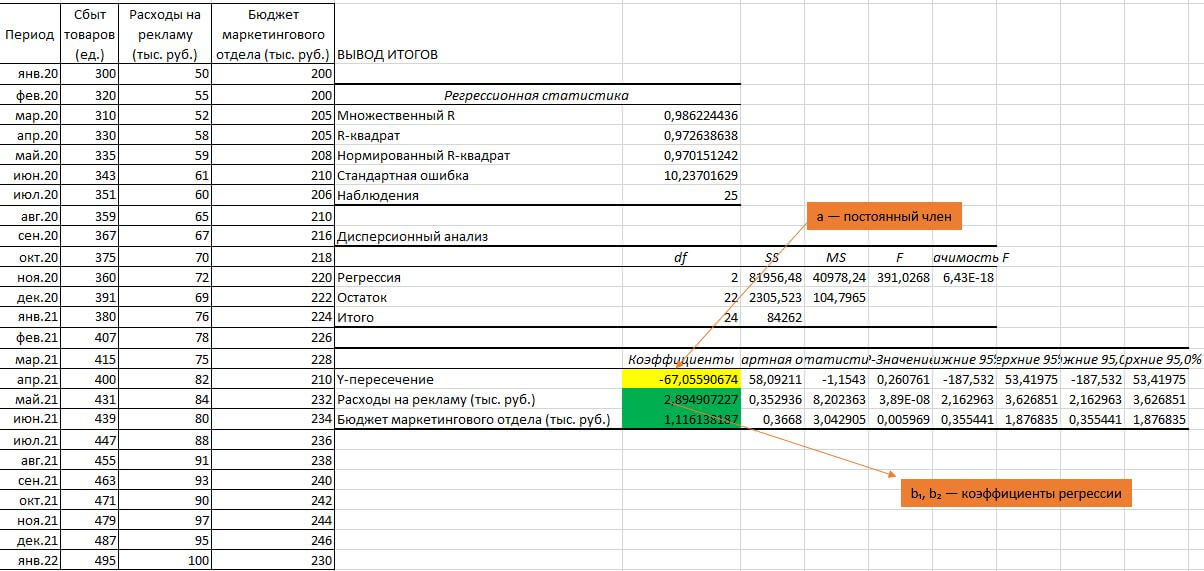
В Excel корреляционно-регрессионный анализ можно провести с помощью инструмента «Регрессия» из Пакета Анализ данных.
На скриншоте ниже показан пример анализа связи между зависимой переменной (сбытом) и независимыми переменными (рекламным и маркетинговым бюджетом). Уравнение регрессии выглядит следующим образом: Y = -67 + 2,89* (расходы на рекламу) + 1,12*(бюджет маркетингового отдела). Подставляя соответствующие числа, можно получить значение продаж за конкретный месяц
Если нужно вычислить степень взаимосвязи между несколькими параметрами, используют корреляционную матрицу (correlation matrix). Это таблица, которая содержит коэффициенты корреляции для каждой пары переменных.
Чтобы построить корреляционную матрицу в Excel, используют инструмент Корреляция из пакета Анализ данных.
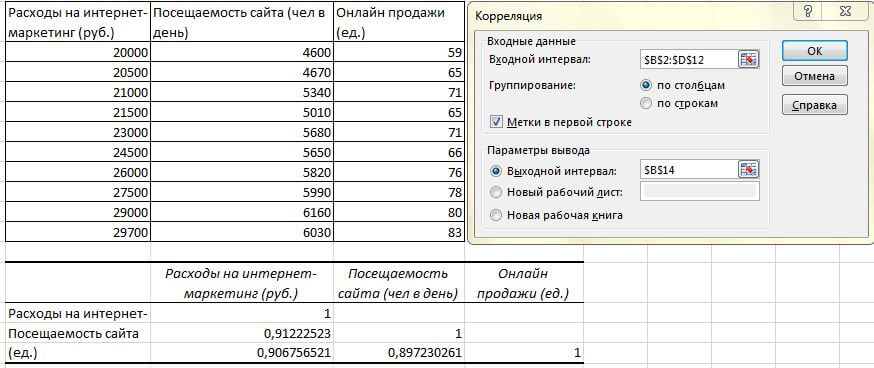
Пример построения корреляционной матрицы в Excel. Определяем взаимосвязь между посещаемостью сайта, расходами на маркетинг и продажами
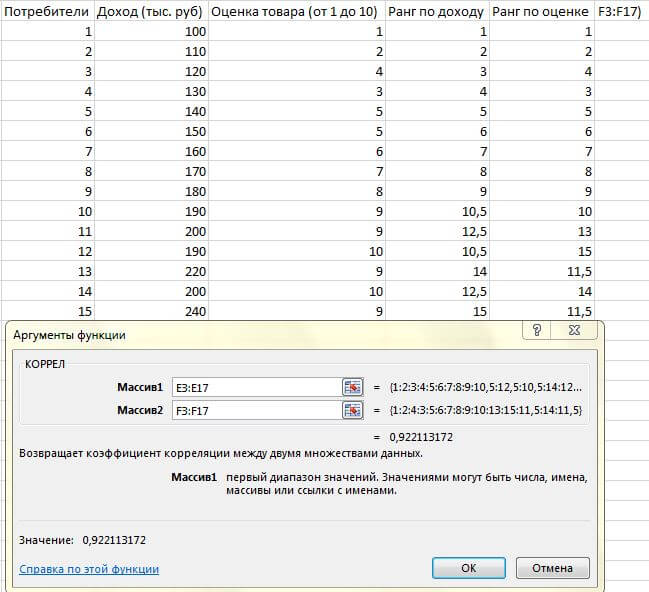
Для определения корреляции можно использовать не только коэффициент корреляции Пирсона, но и ранговый коэффициент корреляции Спирмена. Этот показатель определяет силу и направление связи между двумя группами предварительно ранжированных переменных.
Ранговый коэффициент удобно использовать, когда:
- данные лучше смотрятся в ранговой форме (балльные оценки некоторых критериев, рейтинги или группировка близких числовых значений),
- изменение одной переменной связано с изменением другой переменной, но эта связь не носит линейный характер.
Алгоритм вычисления коэффициента Спирмена в Excel:
- упорядочить две группы чисел;
- использовать функцию РАНГ.СР для ранжирования;
- использовать функцию КОРРЕЛ — как значения в ней берутся ранги.
Ниже приведен пример вычисления рангового коэффициента корреляции Спирмена в Excel
Особенности корреляции, которые важно учитывать при анализе
Не показывает причинно-следственной связи между двумя переменными. Важнейшая черта корреляции. Даже если коэффициент корреляции = 1 (-1), это не значит, что изменение одной переменной приведет к изменению другой.
Есть две переменные: расходы на маркетинг и продажи. Маркетолог вычисляет корреляцию и находит, что она близка к 1. Но ведь продажи могут расти, к примеру, под влиянием сезонного тренда или рекламных акций, а расходы на маркетинг просто удачно вписались в общую картину.
Противоположная ситуация: расходы на маркетинг растут, но идёт спад продаж. Налицо отрицательная корреляция. Но это снова может быть совпадением во времени.
В обеих ситуациях требуется более тщательный анализ: рассмотрение других переменных, учёт сезонности, проверка данных за другие периоды времени.
Может меняться со временем. Например, взяли данные за лето, и они показали слабую корреляцию. Но анализ тех же переменных в зимний период может показать корреляцию, близкую к 1.
Не показывает, какая переменная влияет на другую. Например, расходы на маркетинг могут влиять на показатели продаж. Но ведь и выросшие продажи также могут привести к тому, что топ-менеджеры решат увеличить расходы на маркетинг.
Не показывает зависимость, если она нелинейная. Например, увеличение расходов на маркетинг первоначально приводит к росту продаж. Однако, начиная с какого-то момента, дополнительные расходы больше не стимулируют сбыт, а наоборот, приводят к его снижению (в экономической теории — закон убывающей отдачи).
Приведенные примеры показывают, что вычислить один только коэффициент корреляции мало, нужно более подробно анализировать имеющиеся данные.
Главные мысли: