Теория игр — раздел математики, который изучает стратегии взаимодействия двух и более заинтересованных сторон. Помогает принимать взвешенные и выгодные решения.
Теория игр рассматривает взаимодействие людей как игру. У каждого участника есть несколько вариантов ходов. Выбор стратегии игрока влияет на общую ситуацию, заставляет других вносить коррективы и подстраиваться.
При этом у всех участников есть одна общая цель, которую нужно достичь максимально быстро и с наименьшими потерями. Теория игр учит мыслить логически, рассматривать ситуацию с учетом вероятности, принимать выгодные решения.
Автором концепции считается математик Джон фон Нейман. В 1944 году он совместно с Оскаром Моргенштерном написал книгу «Теория игр и экономическое поведение». Чуть позже теорию развил и дополнил нобелевский лауреат Джон Нэш.
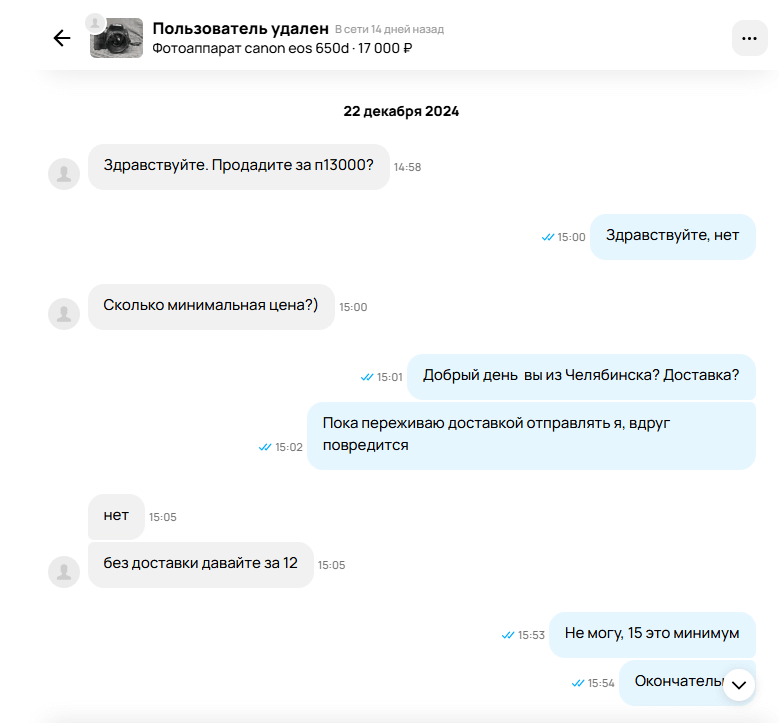
Переписки о скидке на «Авито» — типичная игра. Покупатель и продавец преследуют общую цель — совершить максимально выгодную для себя сделку
Что такое игра
Под игрой здесь понимают любой процесс, в котором несколько участников идут к цели и имеют личный интерес. Это может быть компьютерная стрелялка, переговоры о повышении зарплаты, предвыборная гонка или даже выбор удобного времени для совещания.
Для понимания сути термина рассмотрим бытовую ситуацию. Популярный детский лагерь «Солнышко» продает путевки на летний сезон. Желающих много, а мест ограниченное количество. Путевки можно купить онлайн на сайте либо проехать 100 км и приобрести в бухгалтерии. Старт продаж — в 9 утра 1 мая.
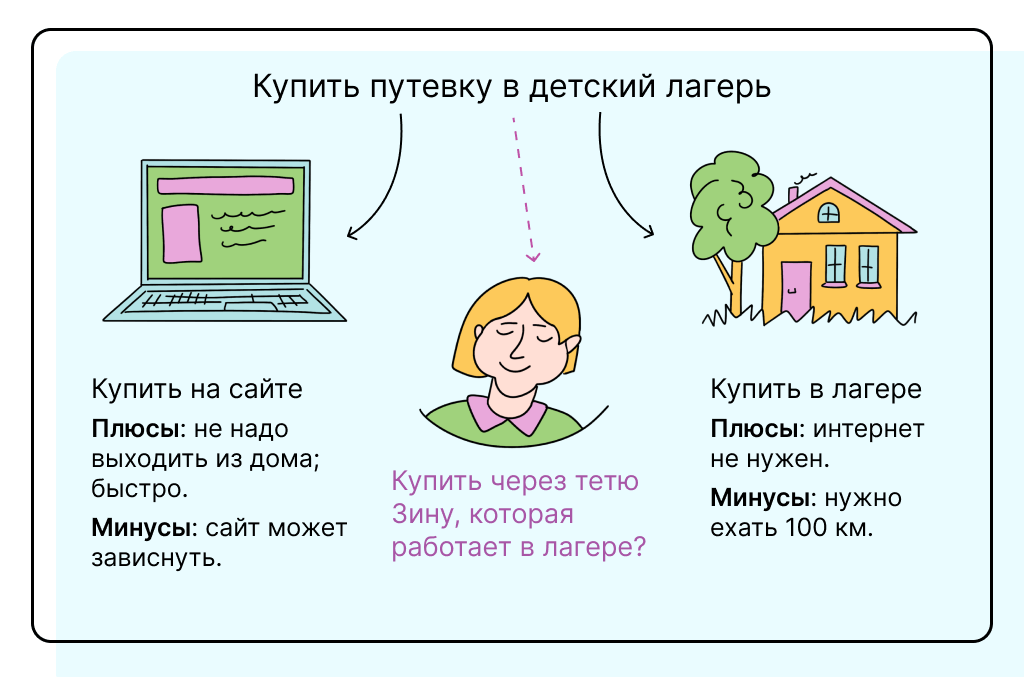
В любой игре всегда присутствуют шесть основных компонентов:
Игроки. Их должно быть минимум двое. В этой ситуации ими будут родители детей.
Цель может быть одинаковой, как в этом случае — купить путевки. Либо разной, но связанной с выгодой для сторон. Например, при переговорах о повышении зарплаты. Начальник не хочет ее поднимать, чтобы сэкономить бюджет. А сотрудник хочет повышения, чтобы купить машину в кредит.
Правила. Это инструкции и возможности для достижения цели. Они могут быть строгими официальными или негласными. В ситуации выше у участников есть два способа достичь цели. Они могут воспользоваться ими либо искать другие обходные пути, например купить путевку через знакомых, которые работают в лагере.
Действия. Набор вариаций, которые можно использовать. Выстраивать стратегии, действовать сообща или по отдельности. Заранее поставить будильник и зайти на сайт за путевкой ровно в 9:00. Либо выехать за пару часов до старта и уже в 8:30 быть около здания лагеря, чтобы первым купить путевку.
Информация. Игроки могут наблюдать и анализировать, как действуют другие участники. Например, видеть количество оставшихся путевок на сайте, обсуждать ситуацию в общем чате, позвонить руководству лагеря.
Взаимосвязанность решений. В любой игре действия одних игроков влияют на других, меняют события и процессы.
Например, если слишком много пользователей зайдет на сайт, он перестанет работать. Тогда выиграют те, кто приехал за путевкой и купил ее в бухгалтерии.
Если основная часть родителей поедут в лагерь на машине, на дороге возникнет пробка, а один бухгалтер не сможет быстро выдать путевки всем желающим. Тогда выиграют те, кто купил их онлайн.

Исход игры сильно зависит от поведения каждого из участников
Теорию игр используют при планировании маркетинговой стратегии, в переговорах и бизнес-решениях. Она помогает мыслить логически, просчитывать на несколько ходов вперед, учитывать вероятность определенных последствий.
Виды игр
С нулевой и ненулевой суммой. В играх с нулевой суммой один игрок забирает приз, а проигравшие остаются ни с чем, как, например, в покере. В играх с ненулевой суммой каждый игрок уносит часть приза, но победитель всегда получает больше других.
Изначально автор теории Джон фон Нейман рассматривал только эти два вида игр. Но уже позже другие авторы дополнили классификацию.
Кооперативные и некооперативные. В кооперативных играх участники объединяются в группы, действуют вместе. Пример — World of Tanks. В некооперативных — каждый сам за себя, как в индивидуальной стометровке на Олимпиаде.
Параллельные и последовательные. В параллельных играх участники действуют одновременно, например, как в сетевой компьютерной стратегии. В последовательных — игроки ходят по очереди, как в шашки.

В Дженге игроки ходят по очереди. При этом от каждого хода соперника зависит исход игры. Важно так убирать брусочки, чтобы усложнить задачу другому участнику, но при этом не уронить башню
С полной и неполной информацией. В первом случае игрок точно знает, какой ход сделал соперник, например как в карточном «дураке». В игре с неполной информацией он либо не знает ничего, либо обладает неполной информацией о ходах других участников. Так происходит в большинстве повседневных человеческих игр, как в кейсе выше про путевки в лагерь.
Симметричные и несимметричные. В симметричных играх у людей одинаковый ограниченный набор стратегий. Чаще всего игроки действуют в замкнутом пространстве, на них минимально влияет окружающая обстановка. Если игроков поменять местами, возможности выбора стратегий не изменятся. Типичный пример — дилемма заключенного. В реальной жизни такие ситуации встречаются редко.
Какие бывают игры
Существует несколько популярных игр, для которых просчитаны оптимальные стратегии. Рассмотрим их подробнее.
Дилемма заключенного
За совместное деяние задержаны два преступника. Они сидят в отдельных камерах без возможности общаться друг с другом. У следователей есть доказательства, чтобы обвинить их в мелком преступлении, но нет улик по крупному нарушению закона. Следствие предлагает каждому сделку:
- Если оба преступника молчат, то каждый получает минимальный срок — 2 года заключения.
- Если один сдает другого, а другой молчит, то сдавший отправится на свободу, а второй преступник сядет на 10 лет.
- Если оба сознаются, то получат по 5 лет.
Чтобы разобрать стратегии и выигрыш каждого с точки зрения теории игр, нужно нарисовать таблицу.
| Игрок 1 сознается | Игрок 1 молчит | |
| Игрок 2 сознается | -5, -5 | 0, -10 |
| Игрок 2 молчит | -10, 0 | -2, -2 |
Максимально выгодной стратегией будет дать показания, потому что в этом случае риски будут минимальны: либо пять лет, либо свобода. А вот молчать невыгодно. Есть риск попасть в тюрьму на 10 лет, и никакой уверенности, что подельник будет так же благороден.
В реальной жизни на исход события будут сильно влиять следователи и родственники заключенных, которые давят на преступников и усиливают сомнения.
Основатель теории Джон Нэш считал, что нельзя отказываться от наиболее выигрышной стратегии ради блага других участников, как в дилемме заключенного. Нужно действовать максимально эгоистично, особенно, если игрок не знает, как поведут себя другие.
Эту ситуацию называют равновесием Нэша. Две доминирующие стратегии уравновешивают друг друга. Каждый игрок получает выигрыш, пусть небольшой, но удовлетворяющий обе стороны.
В маркетинге так работают большинство крупных конкурентов, которые владеют большой долей рынка. Например, Ozon и Wildberries снижают цены и предлагают скидки на сезонные товары. При этом они теряют прибыль, но не допускают массового оттока клиентов к конкуренту.
Охота на оленя
Два человека охотятся на оленя в лесу, где много зайцев. Каждый охотник хочет убить оленя. При этом он может убить зайца лично для себя, спугнув добычу для другого.
Участники могут действовать по отдельности или сообща.
Возможный вариант развития событий иллюстрирует таблица. Если каждый из игроков выбирает вместе охотиться на оленя, оба максимально выигрывают и получают +5 баллов.
Если один из игроков выбирает оленя, а другой зайца, то тот, кто поймает зайца, получит +4 балла, а тот, кто ждет оленя получит 0 баллов. Если оба игрока охотятся на зайца, каждый получает +2 балла.
| Игрок 1 охотится на оленя | Игрок 1 охотится на зайца | |
| Игрок 2 охотится на оленя | 5, 5 | 0, 4 |
| Игрок 2 охотится на зайц | 4, 0 | 2, 2 |
| +5 | +6 |
Стратегия «убить зайца» более выгодна с математической точки зрения. Но если один охотник доверяет другому и у каждого из них достаточно навыков, то лучше договориться убить оленя вместе.
Эту игру в маркетинге хорошо иллюстрируют коллаборации — совместные продукты и активности нескольких брендов. Таким образом они «убивают оленя» — привлекают новых клиентов, обмениваются аудиторией, усиливают узнаваемость. А могли бы довольствоваться зайцами — работать на своих рынках и не рисковать.
Дилемма добровольца
В игре несколько участников, объединенных общей проблемой. Каждый из них может принести небольшую личную жертву ради блага всех игроков. Либо ждать, что это сделает кто-то другой, и терпеть неудобство.
Пример. В микрорайоне отключили свет. Каждый житель может позвонить в управляющую компанию по мобильному телефону. Если никто этого не сделает, свет так и не включат.
Здесь не существует единственно верного решения. Необходимо соотнести объемы затрат с объемами потерь при отсутствии света. Если вам предстоит важный созвон с начальником, то придется потратить время и нервы на звонок. А вот если никаких срочных дел нет, можно подождать инициативы от соседа.
В маркетинге так часто играют конкуренты. Например, фармацевтические компании столкнулись с падением продаж и недоверием аудитории к БАДам. Необходимо развернуть информационную кампанию, рассказать потенциальным клиентам об их пользе, составах, результатах.
Это долго, сложно и дорого. Но при этом если никто из игроков не инициирует просветительский процесс, проиграют все игроки рынка.
Угадай ⅔ среднего
В 2005 году газета Politiken в Дании предложила читателям игру. Любой желающий мог отправить действительное число от 0 до 100. Тот, кто прислал число, близкое к ⅔ среднего арифметического, получал денежный приз.
Логично, что нет смысла отправлять число больше 66, так как две трети максимального числа (100) не может быть больше этого значения. Если так будут рассуждать все участники, они пришлют числа исключительно в диапазоне от 0 до 66. Тогда среднее арифметическое снова снизится и будет приближаться к 44. И так до бесконечности.
Игра полезна с точки зрения оценки группового взаимодействия и умственных способностей участников. Есть мнение, что по итогу игры можно судить об уровне интеллекта участников группы, а также об их мнении о других игроках.
Чем меньшее число в итоге выигрывает, тем выше умственные способности каждого по отдельности и команды в целом. Это значит, что они могут просчитывать варианты развития событий и уверены, что соперники тоже это сделают.
Главные мысли